State Analysis of A Ridge Ventilated Greenhouse
Greenhouse is developed to provide favorable growing environment to plants. Greenhouse environment is set of various parameters which depend on each other. To better understand relation of these parameters on each other i.e. inside condition of greenhouse to those of existing outside environment, various mathematical models have been developed. These models predict the growing conditions as a function of the external climatological variables. Application of these models include the computation of heating and ventilation requirements, the analysis of unconventional designs, the evaluation of different control devices and the testing of new control algorithms
Most of the existing models are based on energy balance method consist of dividing the greenhouse in different elements, modeling the heat and mass fluxes among these elements and generating a heat balance equation for each element. The solution of resulting system of algebraic equations yields the temperature and humidity inside the greenhouse. Assumption used in all these models is that the heat storage capacity of the system is negligible relative to the daily energy input and therefore greenhouse is considered to adjust immediately to the changes in the external environment so that steady state equation may be used.
REVIEW OF WORK DONE AT VARIOUS PLACES
A lot of research work has been carried out on greenhouse technology for the last few decades but very few of them are relevant to Indian climatic condition with fan pad evaporative cooling. Ganguly and Ghosh have presented a thermal model of a fan-pad ventilated floriculture greenhouse to predict the inside greenhouse temperature.
They have also shown the effects of shading and ventilation rate on greenhouse temperature. Shukla et al. have carried out an experimental study to see the effect of an inner thermal curtain in an evaporative cooling system of a cascade greenhouse. A thermal model has also been developed to predict the air temperature. Kittas et al. have shown that the evaporative cooling system is able to keep the greenhouse air temperature at rather low levels. Impron et al. demonstrated that air temperature was affected more by variations of ventilation and leaf area index than by the applied cover properties. The leaf area index had the highest impact on greenhouse air temperature, implying that a large proportion of the cooling is achieved by the crop itself. Sethi and Sharma developed a thermal model for heating and cooling of an agricultural greenhouse integrated with an Aquifer Coupled Cavity Flow Heat Exchanger System (ACCFHES). Kittas et al. reported experimental investigation of the climatic variables of greenhouse such as air temperature, solar radiation, outside wind speed and direction and their interactions affecting the air temperature in a fan-ventilated multi-span greenhouse with rose crop.
Ghosal et al. presented a mathematical model considering heat transfer through flowing water film on shade cloth, stretched over the roofs and south wall of an even span greenhouse to study the effectiveness of cooling in greenhouse.
In the conventional fan-pad evaporative cooling and ventilation system greenhouse fans and the cooling pads are installed on the opposite walls of the house. When outside air is drawn by the induced draught fan in the greenhouse through the wet pad, it gets cooled as latent heat of evaporation of water is taken from the air. This cold air picks up heat while flowing from the pad end to the fan end, causing a temperature gradient along the length of the greenhouse. This puts a restriction on the construction of longer greenhouse.
- CASE STUDY
In this case study, a thermal model of a greenhouse with distributed evaporative cooling is presented. An uneven-span ridge type greenhouse is considered, the fans being aligned along the ridge of the greenhouse and the cooling pads being aligned along the side wall segments .
During the operation, air is drawn by the fans through the wet pads and ventilated out of the greenhouse through the roof. This avoids temperature gradient along the length but a small temperature gradient is set up along the width and height of the greenhouse. Therefore, temperature gradient does not put any restriction on the length of the greenhouse. The study is based on the climate data for the city of Kolkata (22.83°N, 88.82°E), which bears the mixed climatic conditions of the plains and coastal areas of India.
In the present model an east-west oriented, un-even span, single ridge greenhouse has been considered, with a floor area of 180-m2. Fig.15.1 represents the general arrangement of the proposed system. Central and side wall heights of greenhouse are 4 m and 2 m, respectively. The greenhouse is covered with Fiber Reinforced Plastic (FRP). The cooling pads are on the north and south walls, one on each side of each of the six bays or segments. A door is on the west wall and fans are aligned along the ridge of the greenhouse as shown in Fig.15.1. Shade nets are provided along both of the canopy in inclined manner.
- THERMAL MODELING
- Assumptions
- Analysis is considering steady-state condition.
- Heat flow is considered to be one dimensional.
- No energy is absorbed by the structural elements.
- Radiative heat exchange between canopy and side walls has been neglected.
- Input Parameters
- Transmissivity of the covering material for normal beam radiation.
- Transmissivity for diffused and reflected radiation.
- Saturation efficiency of cooling pad.
- Heat absorptivity of Ground.
- Total incident solar energy on greenhouse cover
The total intensity of solar radiation falling on different inclined and vertical surfaces of greenhouse is calculated using solar radiation geometry for the relevant surfaces and solar radiation. The total incident heat load of greenhouse is given by:
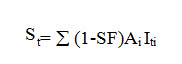
Where Ai is the area of the surface ‘ I’ and Iti is the intensity of transmitted solar radiation into the greenhouse through that surface. The intensity of transmitted solar radiation (It) into the greenhouse can be written as:
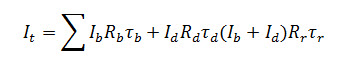
Where Ib and Id are intensity of beam and diffuse radiation respectively. Rb, Rd, and Rr are tilt factors for beam, diffuse and reflected radiation respectively.
τb is the transmisivity of the beam radiation which varies with hour angle and the maximum value is assumed as 0.8 for the material fibre reinforced plastic (FRP). τr and τd are the transmisivity of the global and diffuse radiation which are assumed to be constant and value chosen is 0.76 respectively.
To calculate the total heat load into the greenhouse it is considered that the vertical surfaces receive only diffused radiation because during the peak radiation hours the contribution of beam radiation on the vertical walls is insignificant compared to the total radiation.
- Energy balance equations
- It is considered that the transmitted solar radiation into the greenhouse is fully absorbed by the plants, inside-air and floor of the greenhouse. The temperature inside the greenhouse air can be calculated by applying the law of conservation of energy for the different elements (plant, floor, inside air) of the greenhouse. In the following section energy balance equations for each of the greenhouse components has been presented.
- Greenhouse plants
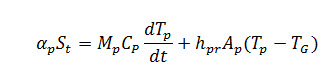
[Rate of energy absorbed by the vegetation]= [Rate of energy used to increase plant temperature]+[Rate of energy convected and evaporated to the surrounding through leaves.]
Where αp is absorptivity of plant suggested Sameshima is given by,
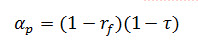
In equation (4) ‘rf’ is the reflectivity of leaves which depends on the variety of plants; ‘τ’ is transmisivity of leaves; ‘hpr’ is convective-evaporative heat transfer coefficient and ‘PT’ is saturation pressure, suggested by Tewari .
- Greenhouse floor
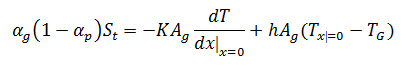
[Rate of energy absorbed by the floor] = [Rate of energy conducted through the floor] +[Rate of energy convected into the greenhouse air]
The rate of thermal energy conducted in the ground is expressed in a steady state condition as
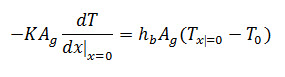
Where, Tx=o is the surface temperature of the ground, °C. Temperature in the ground after a certain depth (Tα) becomes constant and is considered equal to the underground annual temperature, which is assumed to be constant (To) beneath the greenhouse floor as discussed by Tiwari and Goyal [12]. Thus, eqn. can be written as
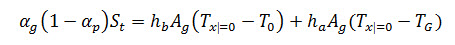
[Rate of energy absorbed by the floor] = [Rate of energy convected from floor to underground] +[Rate of energy convected into the greenhouse air]
- Greenhouse Air
- Assumptions
- The total heat accumulation in the greenhouse air is the summation of transmitted heat after absorption by the plant and floor, convected-evaporated heat from the plants and convected heat from the floor. It is also considered that the heat exchange occurs across the greenhouse covering due to temperature difference between inside and the ambient. If ambient temperature is more than the inside temperature then heat transfer takes place from outside to inside. This total heat increases the inside air temperature and is required to be ventilated out of the greenhouse by ID fans. Thus energy balance equation for the air becomes
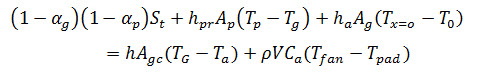
- [Rate of energy gained by the greenhouse air after absorption by plants and floor] + [Rate of energy convected and evaporated in the greenhouse air through plant leaves] + [Rate of energy convected from the floor to the greenhouse air] = [Rate of heat transfer between the greenhouse air and the ambient] + [Rate of sensible heat gain of greenhouse air which is to be ventilated out under steady state condition]
- Where V is the volume of air handled by ID fan and expressed as
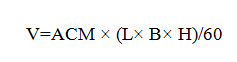
- Where, H is the effective height considering the entire shape of the greenhouse as a parallelepiped. Thus the total volume of air inside the greenhouse is equivalent to the volume of the parallelepiped. Temperature of pads can be expressed as
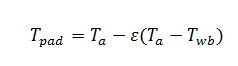
- Where, ε is the saturation efficiency of cooling pads. In equation (8) ‘h’s the overall heat transfer coefficient, given by Sethi [6].
- From Eq. (7) the surface temperature of the floor of the greenhouse (Tx=0) can be written as
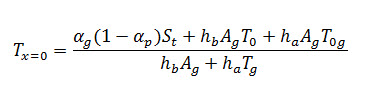
- The average greenhouse air temperature (TG) can be considered to be the arithmetic average of temperature at pad and fan end and Thus
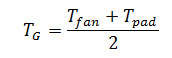
- Combining equations (8), (11) and (12) greenhouse air temperature (TG) can be obtained.
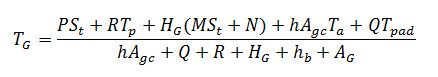
- Considering
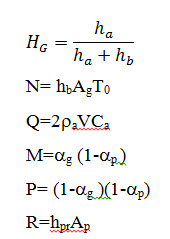
- In simplified form TG can be written as
![]()
- Where
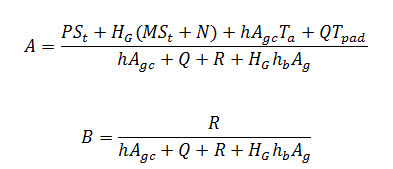
- Combining equation (14) and equation (3) and after simplification it can found as
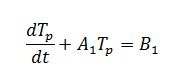
Where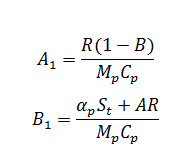
- Solving Eqn. (15) temperature of the plant (TP) can be obtained as
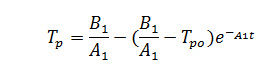
- Where Tpo= initial plant temperature of the greenhouse and ‘t’ is the time in seconds.
- By the value of plant temperature (T), greenhouse air average temperature (TG) can be obtained from Eqn. (14) and fan (Tfan) temperature can be found out from the eqn.(12). Accordingly, temperature gradient along the flow path
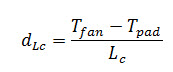
- Considering Lc (length Lc that can be geometrically evaluated by the is the linear distance from the centre of pad to fan which can be calculated greenhouse geometry. It has seen that the average temperature of greenhouse air (calculated by eqn. 14) located above gutter level of shed net . Though greenhouse vegetation below the gutter level therefore it may be considered average air temperature of the effective plantation zone occurs in between the gutter level and pad. From the geometry average greenhouse temperature around plantation zone
![]()
- PERFORMANCE OF THE MODEL
The model performance has been carried out using radiation and temperature data published for Kolkata , assuming a relative humidity. shows the hourly variation of
greenhouse air temperature for a given value of ventilation rate, shading and LAI on 15th May (a representative hot and dry day in summer). At 15 hours of the day when ambient temperature is at the maximum it is seen that using 50% shading, 1.2 ACM ventilation rate and assuming 50% relative humidity a temperature difference of about 7.52°C between ambient and greenhouse air is obtained by using longitudinally pads and fan ventilated distributed evaporative cooling system when LAI is one. Maximum greenhouse air temperature is limited by 28.28°C when the ambient temperature is 35.8°C.
- shows the variation of greenhouse air temperature on 16th August (a representative hot and humid day in the monsoon). The model considers the average hourly radiation intensities for clear sky as the input values. The relative humidity is assumed 75% in this month. It is seen that during hot and humid condition greenhouse inside temperature is well manageable though high relative humidity restricts the temperature reduction by evaporative cooling occurring in the cooling pad. The result arises when greenhouse provides 50% shading, 1.2 ACM ventilation and one LAI.
shows the variation of greenhouse air temperature on 17th January (a representative day in winter). As the thermal load in the month of January is low, ventilation rate of 0.6 ACM is used instead of 1ACM with 50% shading and assuming 50% relative humidity. It is seen that the model predicts the greenhouse inside air temperature below 16°C during the off peak radiation hours in the morning up to 10 a.m.
shows the variation of greenhouse air temperature on 17th January with dry pads. It is seen that greenhouse temperature becomes more than the ambient temperature using the dry run during the winter season. The greenhouse temperature can be maintained between 14.01-24.12°C, a favourable temperature for the plant growth, using 1 ACM ventilation rate with dry pad and 50% shading when LAI is one. Relative humidity assumed to be 50% throughout the day.
It can be concluded that the length of the greenhouse cannot put any restriction for moderating room air temperature. From the analysis it has been shown that
the greenhouse and plant temperature can be maintained satisfactorily throughout the season in a place like Kolkata. In the month of summer the model it is most effective. In winter the model shows very low temperature during the non-peak radiation hours. Thus during those hours in winter natural ventilation with dry pads can be employed.
